La bandera denominada «la estrella de Chile» fue un diseño hermoso y sofisticado , de profunda inspiración masónica, la que con los dos escudos y la guñelve añadidos, y en una escala de 2,4 m de largo, flameó orgullosamente el 12 de Febrero de 1818, día del juramento de la independencia de Chile. Ella fue replicada durante algunos años, pero rápidamente cayó en desuso.
Si se le preguntara a una persona ligada a la matemática cuál es el más hermoso de todos los números, muy probablemente ésta le respondería –tal como yo lo haría- que es el número de oro, aquél que usualmente se denota con la letra griega fi y tiene el valor (√5+1)/2 ~ 1,618… Esta elección puede justificarse a partir de la ciencia misma, pero resulta mucho más inspirador hacerlo desde nuestro entorno, pues el número de oro es omnipresente en la naturaleza. La disposición de las hojas en las plantas (filotaxis), la proporción entre diversas partes del cuerpo humano, la forma de las caracolas de mar, etc., obedecen a patrones ligados a este número. A menudo esto se debe a que en los procesos biológicos rigen leyes de auto-replicación con los cuales está intrínsecamente relacionado. En efecto, este número corresponde a la proporción en la que debe ser dividido un trazo para que el todo sea a la parte más grande como ésta es a la más pequeña. De esta manera, el número de oro corresponde a algo así como un punto de equilibrio al pasar de una escala mayor a otra más chica: «fi» es el número de la armonía.
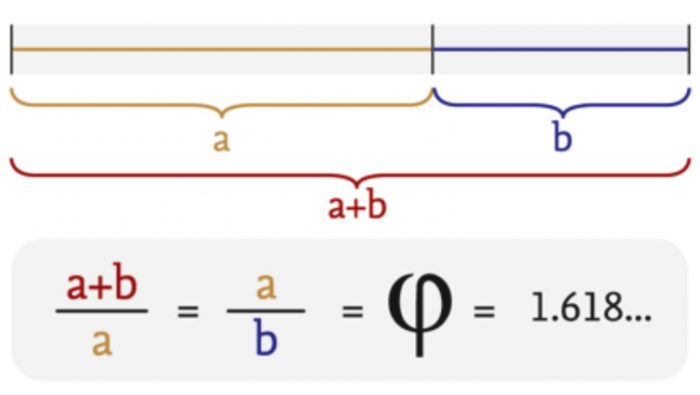
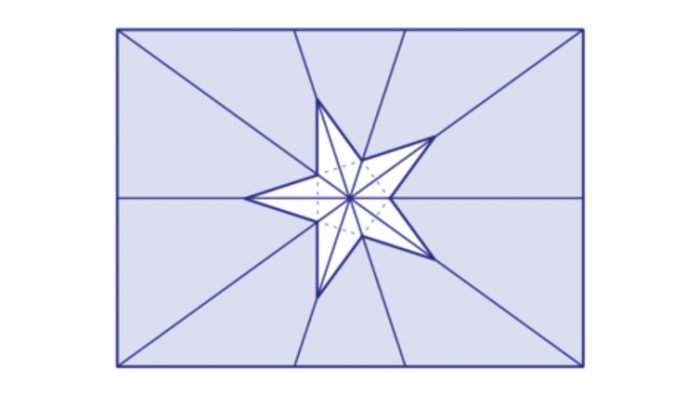
Existen diversos métodos para conseguir una división áurea, pero tal vez el más sencillo está dado por el conocido “triángulo mágico”, aquél de dos ángulos de 72º y uno de 36º. En él, la proporción de los lados mayores respecto del menor es necesariamente igual a fi . Además, si se divide un ángulo de 72º en dos de 36º, entonces la proyección en el otro lado determina también una división áurea. El número de oro aparece así estrechamente ligado a un pentágono regular, pues los triángulos mágicos emergen de él al trazar las diagonales, dando origen a la estrella de cinco puntas.
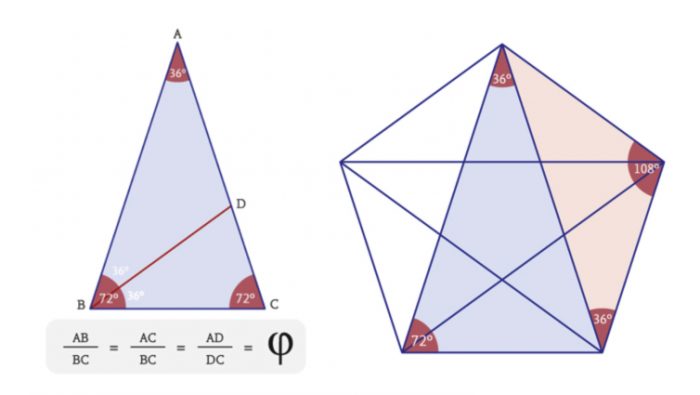
Se tiene antecedentes de la división áurea desde las tablas sumerias del 3200 a.C., en las que aparece asociada a varios pentagramas. Posteriormente, los antiguos griegos lograron comprender de manera sistemática la importancia de fi y su efecto estético, tanto así que lo implementaron en muchas de sus magnas construcciones, como el coloso Partenón de Atenas. De hecho, la notación se estableció en honor a Fidias, creador de varias de las esculturas del templo. Pero quien hizo de la división áurea una pequeña joya de la cultura en Occidente fue el monje matemático Luca Pacione a través de su libro La Divina Proportione (1509). Esta preciosa obra está ilustrada por su gran amigo Leonardo da Vinci, quien incorporó la proporción áurea en la mayoría de sus pinturas, incluida la más sublime de todas: la Gioconda (o Mona Lisa). Su simple contemplación nos hace olvidar toda sugerencia a códigos secretos o teorías conspirativas para sobrecogernos ante su bella e insinuante sonrisa. En ésta, subyace la perfección de la geometría euclidiana encapsulada en un único y prístino número que no deja de maravillar a artistas, arquitectos, místicos, poetas y científicos: fi.
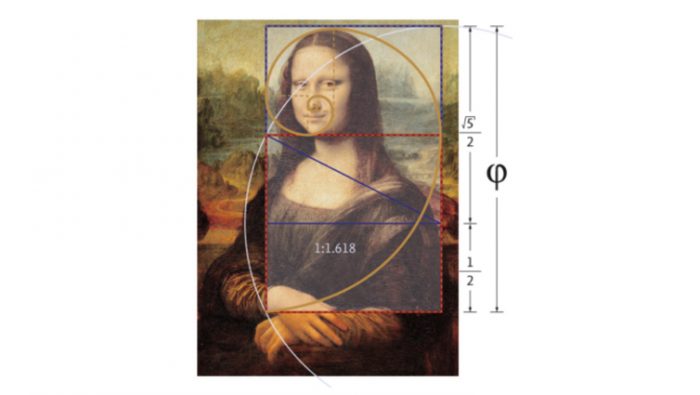
Increíblemente, pese a su relevancia universal, es ampliamente ignorado en nuestro país que el número de oro está anclado también en lo más profundo de nuestra historia, más precisamente, en el diseño de nuestra bandera nacional, la “estrella de Chile”.
Por mandato de Bernardo O’Higgins, la elaboración de la bandera de la Patria Nueva fue responsabilidad de Ignacio Zenteno, quien al parecer encargó el diseño a Antonio Arcos (hay quienes señalan que éste fue realizado por Gregorio de Andía y Varela), siendo la confección de la primera de ellas obra de Dolores Prats de Huici (algunos señalan a las hermanas Pineda de Concepción). Si bien la estructura y los colores son similares a los de hoy, varios detalles distintivos llaman la atención. Primeramente, constaba de dos escudos diferentes al centro (uno por cada lado). Por otra parte, incorporaba –dentro de la estrella pentagonal– una de ocho puntas, la guñelve, que en la tradición mapuche representa al planeta Venus y que fue usada por Lautaro en su pendón de guerra. Pero las diferencias no se detienen allí: las dimensiones de esta bandera eran muy distintas a las de la actual, pues estaba concebida en función de la razón áurea. Si bien no se dispone de ningún documento oficial al respecto, algunas personas se han interesado en el tema. De entre ellas, Gastón Soublette exhibió varios de estos aspectos en su hermoso libro “La Estrella de Chile” (1984). Sin embargo, consideraciones conceptualmente más actualizadas y mediciones más acabadas permiten corregir algunos errores y desentrañar completamente el diseño, de una belleza y elegancia geométricas deslumbrante.
En primer lugar, el alto de la bandera se divide horizontalmente en dos partes iguales: la inferior para el campo rojo, y la superior para los campos blanco y azul. La proporción entre los largos de los campos blanco y azul es exactamente fi . En el campo azul, la proporción entre el alto y el largo es igual 0,72654… Esto permite que las diagonales del rectángulo azul formen en su centro, hacia izquierda y derecha, dos ángulos de 72º (el valor 0,72654… no es otra cosa que la tangente de 36º). Este aspecto es sumamente importante, pues 72º corresponde a la quinta parte de una circunferencia completa. La estrella de cinco puntas comienza así a delinearse.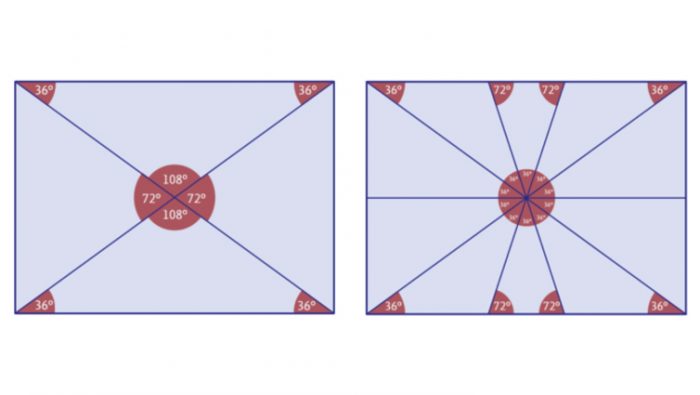
Pero aún falta lo más impresionante: los ángulos que quedan en la intersección de las diagonales apuntando hacia arriba y abajo son de 108º, que al ser divididos cada uno en tres partes iguales de 36º nos determinan dos pares de triángulos mágicos; además, los lados de los ángulos centrales de 36º cortan a los segmentos horizontales superior e inferior en razón áurea. Si se traza ahora la horizontal media del campo azul, por el centro del rectángulo pasarán cinco líneas que forman consecutivamente ángulos de 36º. De esta forma, eligiendo alternadamente cinco puntos en estos trazos sobre una circunferencia basada en el centro, tendrá los vértices de una estrella pentagonal totalmente regular, con una inclinación dinámicamente sugerente hacia los vértices del campo azul. Un último detalle: la magnitud de la circunferencia parece haber sido escogida de modo que la razón entre el alto del campo azul y el diámetro de ésta sea nuevamente igual a fi.
Fue esta hermosa y sofisticada bandera, de profunda inspiración masónica, la que con los dos escudos y la guñelve añadidos, y en una escala de 2,4 m de largo, flameó orgullosamente el 12 de Febrero de 1818, día del juramento de la independencia de Chile. Ella fue replicada durante algunos años, pero rápidamente cayó en desuso. Su fin era mera cuestión de tiempo al no existir una elite que fuese capaz de apreciar y entender su belleza y contrapesarla a la dificultad de su elaboración. Basta señalar que, incluso en 1960, el historiador Luis Valencia Avaria la describía como siendo “de tamaño desproporcionado por su extraordinario largo”…
El nacimiento definitivo de la bandera actual derivó de una ley dictada en 1912: “La proporción entre el alto y el largo –o vaina y vuelo– de la bandera chilena debe ser 2:3, quedando dividida horizontalmente en dos franjas de igual tamaño. Mientras el sector inferior corresponde al color rojo, el sector superior se subdivide a la vez en un cuadrado azul y un rectángulo blanco, cuyos largos están en proporción 1:2, respectivamente. La estrella se ubica en el centro del cantón azul y se elabora sobre una circunferencia cuyo diámetro corresponde a la mitad del lado del cantón”.
Nacía así una bandera que, comparada con la original, no puede parecernos sino rígida, simplista y despojada de simbolismo. Desaparecía con esto la “primera estrella de Chile”, aquélla diseñada magistralmente como un emblema del portentoso destino que para nuestra patria soñaron nuestros próceres. ¿No será esto una pequeña metáfora de nuestra historia?
Juzgue usted: ¿cuál es más armoniosa?
La bandera del día de la independencia se conserva en el Museo Histórico Nacional. En 1980 fue secuestrada por el MIR, simbolizando con ello el secuestro del ideario republicano que llevó a cabo la Dictadura. Fue devuelta en 2003 por la Agrupación de Familiares de Detenidos Desaparecidos –con intermediación del equipo del semanario The Clinic– y restaurada en 2009. Agradezco infinitamente a todo el personal del museo, en especial a Fanny Espinoza, por toda la información proporcionada, así como por el permiso para examinarla y corroborar los aspectos geométricos descritos: fue un momento emocionante.
Fotografía de la bandera de la independencia tal cual es conservada hoy en el museo. No está de más decir que ninguna de las restauraciones a las que ha sido sometida ha tenido especial cuidado de su innegable valor geométrico, de modo que sus dimensiones actuales son diferentes a las de su concepción original.
Andrés Navas. Universidad de Santiago de Chile. Presidente de la Sociedad de Matemática de Chile.
