CULTURA|CIENCIA
Galileo, Newton, Einstein… apenas tres de los grandes de la ciencia occidental.
Pero como el mismo Newton escribió, citando al erudito del siglo XII Bernardo de Chartres, «Si he visto más lejos es porque estoy sentado sobre los hombros de gigantes».
Varios de esos gigantes sobre los que se sentaron y se siguen sentando los científicos, han quedado en un olvido relativo… aunque a veces, si nos fijamos con cuidado, los encontramos en las páginas de los gigantes conocidos.
Según los historiadores, el mayor legado del gran matemático italiano, Leonardo Pisano, más conocido como Fibonacci, fue ayudar a Europa a descartar el antiguo sistema de números romanos y cambiarlo por números indo-arábigos.
Aparecieron en su «Liber Abaci» o «Libro de cálculo», que escribió en 1202 tras estudiar con un maestro árabe.
En ese mismo libro, hay una referencia a un texto anterior llamado «Modum algebre et almuchabale» y en el margen está el nombre Maumeht, que es la versión latinizada del nombre, Mohammed.
Como Fibonacci, los eruditos europeos del siglo XII al XVII se refieren regularmente a textos islámicos anteriores y nombres árabes aparecen en escritos sobre temas tan variados como óptica, medicina y cartografía
La persona a la que se refiere es Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī, conocido en español como Al-Juarismi, quien vivió aproximadamente entre los años 780 y 850.
Fue gracias a él que los intelectuales europeos se enteraron de la existencia de los números indo-arábigos.
La obra de Al-Juarismi toca un aspecto crucial de todas nuestras vidas.
Por ella, el mundo europeo se dio cuenta de que su forma de hacer aritmética, que todavía se basaba esencialmente en números romanos, era irremediablemente ineficiente y francamente torpe.
Si te pidiera que multiplicaras 123 por 11, podrías hacerlo hasta en tu cabeza. La respuesta es 1.353.
Pero intenta hacerlo con números romanos: tienes que multiplicar CXXIII por XI.
Se puede hacer pero, créeme, no es divertido.
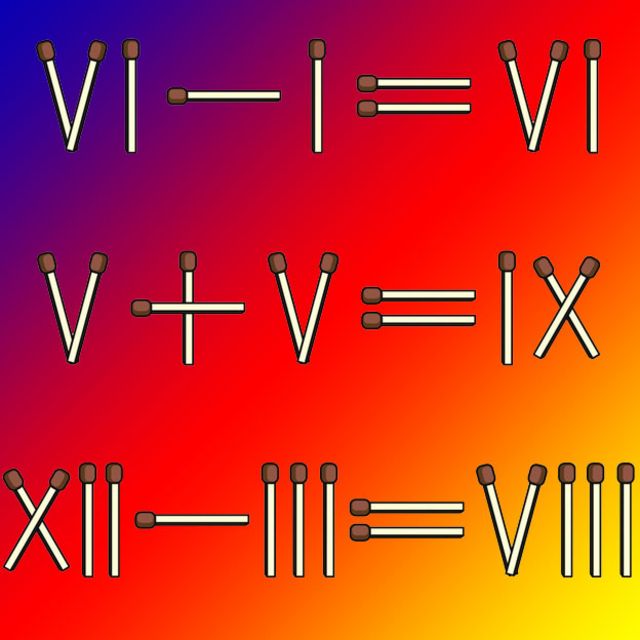
Ni siquiera sumar y restar es igual de fácil pero, ¿notaste que estas ecuaciones son incorrectas? Si quitas sólo un fósforo las corregirás (respuestas al final)
En su «Libro de la suma y de la resta, según el cálculo indio», Al-Juarismi describió una idea revolucionaria: se puede representar cualquier número que desee con solo 10 sencillos símbolos.
Esta idea de usar solo diez símbolos -los dígitos del 1 al 9 más un símbolo 0- para representar todos los números desde uno hasta el infinito, fue desarrollada por matemáticos indios alrededor del siglo VI y es difícil exagerar su importancia.
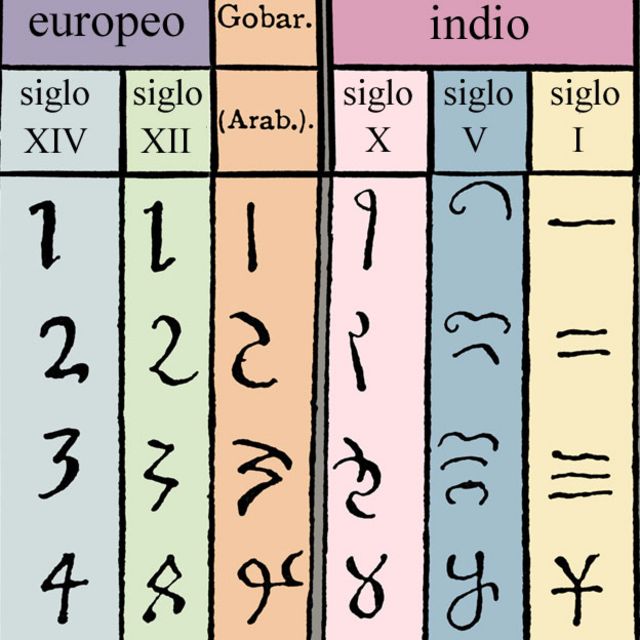
Así fueron cambiando, de derecha a izquierda
Al-Juarismi y sus colegas hicieron más que traducir el sistema indio al árabe: crearon el punto decimal.
Lo sabemos gracias a la obra del matemático Abu’l Hasan Ahmad ibn Ibrahim Al-Uqlidisi.
En «Kitab al-fusul fi al-hisab al-Hindi» de los años 952-3 –el manuscrito más antiguo en el que se propone un tratamiento de las fracciones decimales, escrito apenas un siglo después de Al-Juarismi- muestra que el mismo sistema decimal se puede extender para describir no solo los números enteros sino también las fracciones.
La idea del punto decimal nos resulta tan familiar, que es difícil entender cómo antes se las arreglaban sin ella.
Como toda gran ciencia, es deslumbrantemente obvio después de haber sido descubierto.
El cero y el punto decimal nos llevaron al infinito. Un gran ejemplo es el número de Euler, uno de los más importantes en matemáticas. Actualmente se calcula con más de 1 billón de dígitos de precisión, se conoce principalmente como la base de los logaritmos naturales y para su uso en el cálculo del interés compuesto
Al-Juarismi, el gran matemático que le dio a Occidente los números y el sistema decimal, era además astrónomo, cortesano y favorito del Califa al-Mam’un.
Era un emigrante de Persia oriental a Bagdad y producto de su época, la Edad de Oro del islam.
Su manera de pensar era audaz y gozaba de un gran un lujo: estaba rodeado de libros.
Como todas las grandes figuras del imperio islámico, Al-Juarismi vivió en una cultura sin retratos. Las poquísimas imágenes que tenemos son impresiones posteriores de cómo podría haber sido
Gracias al Movimiento de la traducción, que recogió obras científicas de todo el mundo conocido, a fines del siglo IX, un importante corpus matemático griego -que incluía obras de Euclides, Arquímedes, Apolonio de Perga, Tolomeo y Diofanto- había sido traducido al árabe.
Del mismo modo, las matemáticas antiguas babilónicas e indias, así como las contribuciones más recientes de los sabios judíos, estaban disponibles para los estudiosos islámicos.
Al-Juarismi se encontraba en la sorprendente posición de tener acceso a diferentes tradiciones matemáticas.
La griega trataba principalmente de la geometría, la ciencia de formas como triángulos, círculos y polígonos, y cómo calcular el área y el volumen.
La india había inventado el sistema decimal de diez símbolos que hacía el cálculo mucho más simple.
Al combinar la intuición geométrica con precisión aritmética, imágenes griegas y símbolos indios, inspiró una nueva forma de pensamiento matemático que hoy llamamos álgebra.
Al-Juarismi le dio el nombre y contenido a álgebra
En el libro de Al-Juarismi «Al-Jabr w’al-Muqabala» es la primera vez que aparece la palabra Al-Jabr. Álgebra.
Empieza diciendo: «Descubrí que las personas requieren tres tipos de números: unidades, raíces y cuadrados».
Así te prepara para un libro sobre cómo resolver ecuaciones mediante métodos algebraicos.
Ya en los tiempos de Babilonia se resolvían ecuaciones cuadráticas.
La diferencia es que no había fórmulas, sino que cada problema se resolvía como único: «Toma la mitad de 10, que es 5, y el cuadrado, que es 25»; y más adelante, otro diría: «Toma la mitad de 12, que es 6, y el cuadrado, que es 36».
Así sucesivamente, te hacían pasar por el mismo proceso una y otra vez con diferentes números, según el caso.
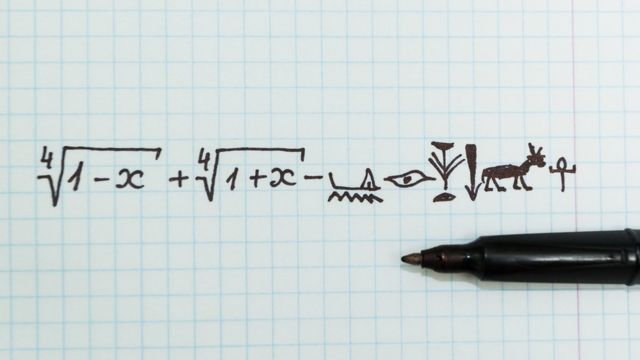
Las fórmulas liberan pues ofrecen una manera solucionar el mismo tipo de problemas sin tener que repensarlos desde el principio cada vez
Para Al-Juarismi, la solución no se eran números que debíamos descubrir, sino un proceso que pudiéramos aplicar.
Es decir: el cuadrado significa tomar la raíz y multiplicarla por sí misma. Y esa fórmula es cierta, cualquiera que sea la raíz. Si es 5, es 5 veces 5, es 25; si es 3, es 3 veces 3…
No usar números sino símbolos resultó ser una idea increíblemente liberadora, pues permite resolver problemas sin atascarse en cálculos numéricos desordenados.
Algoritmi de número Indorum
Al abandonar temporalmente el enlace con números específicos, manipulas los nuevos objetos (x, y, z) de acuerdo a las reglas que su libro explicó: una serie de recetas generales.
Los números que los símbolos representan en tu problema particular aparecerán milagrosamente al final.
Piensa en algo sencillo y cotidiano, que era lo que Al-Juarismi quería ayudar a resolver:
Ahmed muere y deja 80 monedas de herencia. A un amigo le deja un cuarto de ella; a su viuda, un octavo; lo demás es para sus tres hijos. ¿Cuánto le corresponde a cada uno de ellos?
Al Juarismi hizo que lo desconocido fuera parte de la ecuación: lo que llamamos X en algebra. Entonces:
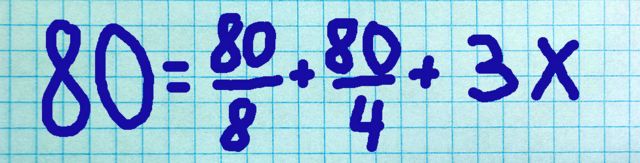
El tratado escrito por Al-Juarismi circa 825 sobre el sistema numérico indio-árabe fue traducido en el siglo XII con el nombre «Algoritmi de numero Indorum«, que significa «Algoritmi sobre los números de los indios»; «Algoritmi» fue la latinización del traductor del nombre Al-Juarismi.
En él nos dio esas recetas que, debido a esa traducción de su nombre, terminaron llamándose algoritmos.
Al-Juarismi hizo posible que el álgebra existiera como un área de las matemáticas por derecho propio, y que se convirtiera en un hilo unificador de casi todas las demás.
El álgebra es una hermosa serie general de principios, y si los comprendes, la entenderás.
Se ha utilizado a lo largo de las eras para resolver todo tipo de problemas.
Si la masa de una bala de cañón es ’m’, y la distancia que tiene que viajar, ‘d’, usas álgebra para calcular el ángulo óptimo en el que tienes que apuntar tu cañón.
Ese tipo de conocimiento gana guerras.
O llamemos a la velocidad de la luz ‘c’, el cambio en la masa de un núcleo atómico ‘m’, y luego calculemos la energía liberada con esta sencilla fórmula algebraica:
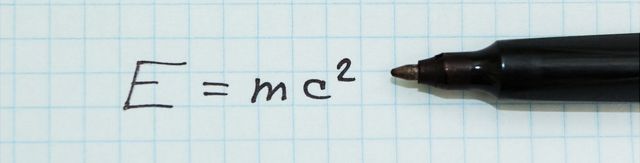
La ecuación más famosa, la equivalencia entre la masa y la energía dada por la expresión de la teoría de la relatividad
Ese tipo de conocimiento es el poder real.
